1 概述
渲染过程中最基础的要数光栅化过程,什么是光栅化?简单来说光栅化就是建立一个连续光滑图元到屏幕中离散像素的映射,这个过程中包括 2d 图元和 3d 图元,后续分别展开讨论
2 点和像素
在平面或者空间中的点怎样算是命中像素或者,可以被像素对应的像素点采样并绘制
2.1 难点/目标
- 定位点的边界
3 直线绘制
已知平面内两个点,如何快速高效的将两点及两点之间的点绘制在屏幕当中
3.1 难点/目标
- 高效快速
- 点于点之间的像素插值
3.2 算法实现
这里主要有两种计算方式分别面向直线的几何特点插值的 bresenham 算法和面向像素积分的理念 dda 积分算法。作为整个渲染过程中最为基础的环节,直线绘制算法的效率至关重要,因而我们着重演示算法的演进过程以尽可能的提高算法的执行效率 (现代编译器已经足够智能,部分优化实现会被在开启 o2 或者 o3 优化后由编译器自动实现)
3.2.1 Bresenham 算法
首先最直接的我们从直线的几何表示出发已知像素空间中直线上两点 $(x_0,y_0) (x_1,y_1)$,我们可以得到这条直线的的表示
$$ y - y_0 = \frac{y1-y0}{x1-x0} (x - x_0) $$
有了直线的定义,下一步确定像素点在直线的位置,首先我们我们可以定义一个固定的步长增长,对 x 和 y 分别按照相同的步长比例进行插值。得到我们中间的点 xy
$$ \begin{cases} x = x_0 + step * (x_1 - x_0) \newline y = y_0 + step * (y_1 - y_0) \end{cases} $$
float delta = 0;
while (delta <= 1.0F) {
float x = x0 + delta * (x1 - x0);
float y = y0 + delta * (y1 - y0);
image.set(x, y, color);
delta += 0.01;
}
需要注意的是在插值过程得到的点可能和实际像素存在差异,要注意像素点的采样
通过固定步长我们发现很难选择一个固定的步长满足不同场景下的需求,步长太小单个像素执行了过度的计算浪费了计算资源。步长太大,实际渲染的直线存在断点缺口等不连续的问题
我们容易想到既然我们实际是绘制到像素中,以像素变化取代固定的步长无疑是一个合适的做法。我们可以基于两点坐标,按照 x 或者 y 方向步进像素,并基于两点式计算另一个点的坐标
$$ \begin{cases} x_{current} = x_{last} + 1 & \newline y_{current} = y_0 + kx, & 其中k = \frac{y1-y0}{x1-x0} \end{cases} $$
3.2.2 dda 积分算法
在 Bresenham 算法最后我们使用基于像素步进的方式计算着色像素的坐标点,但是乘法操作相对于加法操作还是有更多的的开销,同时每个像素其是连续的我们可以基于积分思想,确定当前累计的变化是否可以步进一个单位像素,如下所示,当累计的 delta 大于大于 0.5 时,我们认为其递增超过像素和像素间的界限此时,$y = y + 1$
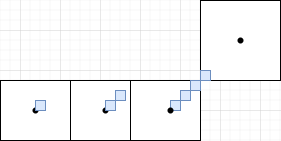
同时对于累积项 delta 减去一个单位像素
$$ \begin{cases} x = x + 1 \newline delta = delta + k, 其中k=\frac{y_1-y_0}{x_1-x_0} \end{cases} $$
算法伪代码
int dx = x1 - x0;
int dy = y1 - y0;
float eps = float(dy) / float(dx);
float eps_sum = 0;
while (x0 < x1) {
eps_sum += eps;
if (std::abs(eps_sum) > 0.5) {
y0 += (y1 > y0) ? 1 : -1;
eps_sum += eps_sum > 0.5 ? -1 : 1;
}
x0 = x0 + 1;
}
进一步优化,像素累积过程我们实际上可以考虑使用整数加法替代浮点数运算,其实质就是实际增长的数据大小是否超过我们的分母,同时像素和像素之间的边界也需要发生变化。
最后给出工程化代码实现,相对于算法理论实际操作中要考虑更多的内容
- 步进的方向的选择,满足单调递增的性质
- 步进坐标轴的选取使其满足步进坐标轴的增长速度快于次坐标轴的增长速度,否则增长速度过快使得一个像素步进对应多个像素的绘制
实际代码
bool is_reverse = false;
if (abs(y1 - y0) >abs(x1 -x0)) { // 确定按照XY次序步进,若k<1则按照x步进,反之按照y步进,通过Swap后下文可以均按照x步进
std::swap(x0, y0);
std::swap(x1, y1);
is_reverse = true;
}
if (x0 > x1) { // 单调递增
std::swap(x0, x1);
std::swap(y0, y1);
}
int dx = x1 - x0;
int dy = y1 - y0;
int eps = abs(dy * 2);
// 替代之前求斜率的想法,取而代之的是直接和分母对应的整数比较,注意后续比较范围为-0.5 ~ 0.5 可以取斜率绝对值简化逻辑,
int eps_sum = 0;
int y = y0;
while (x0 < x1) {
if (is_reverse) {
image.set(y, x0, color);
} else {
image.set(x0, y, color);
}
eps_sum += eps;
if (eps_sum > dx) { // 因为其只关心增长速度不关心增长方向,为避免小数使用*2转化为对应的原始分母
y += (y1 > y0) ? 1 : -1;
eps_sum -= 2 * dx; // 注意是两倍的dx
}
x0 = x0 + 1;
}
4 三角形绘制
明确直线绘制的方法后,我们再进一步,对于最基础的三角形图元,我们可以利用之前提到的直线绘制
4.1 难点
- 重心插值算法
4.2 线框绘制
非常自然,已知三角形的三个顶点,我们可以绘制三角形线框
4.3 实心三角形绘制
实心三角的绘制主要可以使用扫描转化和包围盒光栅化算法两种算法采用了不同的实现思路
4.3.1 扫描转化光栅化
扫描转化算法主要基于像素是一个个连续排列的栅格思想,按照三角形顶点按照 y 排序,确定在当前 y 中 x 的左右两个边界,依次遍历并进行着色
if (t0.y == t1.y && t0.y == t2.y)
return;
// t0 < t1 < t2
if (t0.y > t1.y)
std::swap(t0, t1);
if (t1.y > t2.y)
std::swap(t1, t2);
if (t0.y > t1.y)
std::swap(t0, t1);
int height = t2.y - t0.y;
int half_height = t1.y - t0.y;
for (int i = 0; i <= height; i++) {
float alpha = float(i) / float(t2.y - t0.y); // t0 - t2
int left = alpha * float(t2.x - t0.x) + t0.x;
if (left < 0) {
int x = 1;
}
if (i <= half_height && t1.y != t0.y) {
float beta = float(i) / float(t1.y - t0.y); // t0 - t1
int right = beta * float(t1.x - t0.x) + t0.x;
if (left > right)
std::swap(right, left);
for (int j = left; j <= right; j++) {
image.set(j, i + t0.y, color);
}
} else {
float beta = float(i - half_height) / float(t2.y - t1.y);
int right = beta * float(t2.x - t1.x) + t1.x;
if (left > right)
std::swap(left, right);
for (int j = left; j <= right; j++) {
image.set(j, i + t0.y, color);
}
}
}
4.3.2 包围盒光栅化算法
包围盒光栅化的思想很简单,对于任意一个三角形其可以认为被一个包围盒包裹如下所示,从包围盒中我们可以快速获得当前这个三角形的上下左右临界。更进一步如果我们了解到在这个包围盒中,那些部分属于三角形内部,哪些部分属于三角形外部,我们就可以绘制出三角形图元。
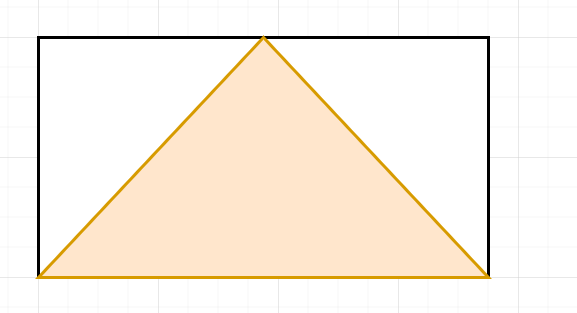
所以问题转化成为,已知三角形三个顶点坐标,和任意一点,如何判定当前点是否在三角形内部和外部,在这里使用了三角形重心坐标(barycentric)判定像素点和三角形顶点之间的关系,具体内容参照 [[插值算法]]
if (verts[0].y == verts[1].y && verts[1].y == verts[2].y)
return;
vec2 bboxmin(image.width() - 1, image.height() - 1);
vec2 bboxmax(0, 0);
vec2 clamp(image.width() - 1, image.height() - 1);
for (int i = 0; i < 3; i++) {
bboxmin.x = std::min(bboxmin.x, verts[i].x);
bboxmin.y = std::min(bboxmin.y, verts[i].y);
bboxmax.x = std::max(bboxmax.x, verts[i].x);
bboxmax.y = std::max(bboxmax.y, verts[i].y);
// 防止溢出
bboxmin.x = std::max(0.0, bboxmin.x);
bboxmin.y = std::max(0.0, bboxmin.y);
bboxmax.x = std::min(clamp.x, bboxmax.x);
bboxmax.y = std::min(clamp.y, bboxmax.y);
}
for (int i = bboxmin.x; i <= bboxmax.x; i++) {
for (int j = bboxmin.y; j <= bboxmax.y; j++) {
// Vector X
// barycentric
vec3 p =
barycentric(verts, {static_cast<double>(i), static_cast<double>(j)});
if (p.x < 0 || p.y < 0 || p.z < 0)
continue;
image.set(i, j, color);
}
}