1 解决什么问题?
解决空间中物体快速判断和射线的相交问题。通过树形的方式将物体组织起来,树的 Parent 对应的 Volume 包围 Child 物体所处的空间,实现一种层次化的组织结构,避免逐一判断物体和射线是否相交。
父级下的子 Volume 间可能存在相交的情况,对于每个叶子节点也就是实际物体,其应该唯一地属于一个 Volume
2 作用在那些场景
由于 BVH 提供点到物体的快速求交,因而可以应用于以下情景
- 碰撞检测
- 交互拾取
- 光线追踪
- 视椎体剔除
- 遮挡判断
- 最近邻居发现
3 如何实现
3.1 基于 AABB 包围盒实现
基于 AABB 包围盒实现快速判断相交的算法也称为 Slabs Method 。
3.1.1 Base
问题的定义 我们首先关注包围盒的核心功能快速求交,这个问题本质上是一个区间求交的问题,即在三维空间中判断射线所处的空间和包围盒所处的空间存在交集。
对于一个一维空间问题,这个是一个区间重叠的判断,对于二维空间,问题转化为 xy 轴区间构成的矩形区域和矩形区域相交的问题。而三维中,变成了三个坐标轴所构成的空间和空间重叠的问题。
通过观察这个过程我们可以发现,不管是一维、二维还是三维,我们总能够将其进行分解,将问题转化为一维的问题,即问题最终变为,不同维度的一维区间求交,且所有维度均存在交集,我们才认为两个空间存在交集。
区间求交 在一维空间中,点和区间中的判断是非常简单,仅仅需要比较点和边界,但是区间和区间之间的关系较为复杂,可以分为
- 区间内
- 区间相交
- 区间外
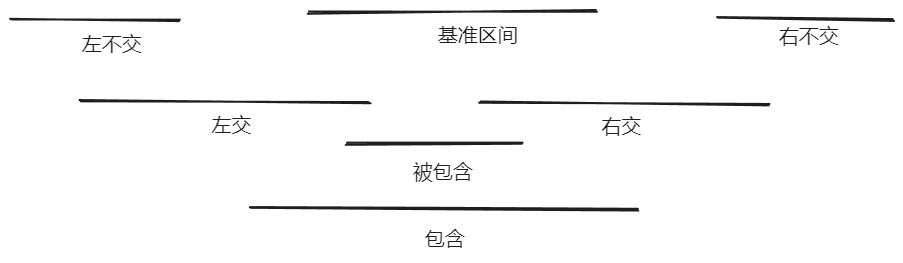
前两中情况都是区间重叠的情况,最后一种情况是区间互不想干的情况 (左不交和右不交),因而我们关注其和基准区间的关系,发现其特殊在临界值的比较上,当两个区间存在交集的时候两个区间的左临界均小于两个区间的右临界,进一步我们观察区间外的情况发现其存在区间的左临界大于有临界的情况
3.1.2 建树
解决 AABB 包围盒判定的问题后下一步就是包围盒和包围盒间的组织建树过程
在一维下,我们可以直接排序按照次序构建层级关系,但是在三维中,我们有三个重要性相同的问题,因而很难用排序去解决这个问题,一种经典的自上而下分治的方法,每次随机抽取一个坐标轴,然后排序,将序列进行均分,形成特定的序列。
- 计算覆盖参与 BVH 节点计算的所有物体的 BoundingBox,并保存
- 若此时仅有一个物体
- 标记为叶子节点
- 若此时只有两个物体
- 分别作为左右孩子继续构建
- 其他情况,按照随机选择的坐标轴排序,划分为两个序列递归建树
在这个过程中,那些指标影响我们最终 BVH 的效果呢?从直观的角度来说,树的左右两侧在空间中分布越均匀,效果越好。但是实际情况比较复杂,我们很难高效地做到空间中的均匀分布,因而一个折中的方式就是在次序上做分割。
随机显然不是最优解,另一个非常直觉的优化时,选择三个轴的最长长度最为当前划分轴,这种方法相比于之前的随机选择坐标轴无疑更容易使得划分过程中的空间均匀分布
3.1.3 计算
这里以光线追踪为例,如何判定射线和空间中的某个区域存在交集?前面提到,我们可以将三维空间按照 XYZ 分解转化为一维的区间问题,对于包围盒分解非常简单,对于光线而言怎样分解较为合适?在这里光线我们定义为,其中 O 是起点,d 代表光线方向
$$ ray = O + td $$
在光线的计算过程中,我们会对光线的传输限定一个范围 R,保证光线求交的正确性,因而我们可以基于这个范围的临界条件计算光线传输过程在空间中的范围
$$ \begin{cases} x:[O_x+R_{min}\cdot d_x,orgin_x+R_{max}\cdot d_x] \newline y:[O_y+R_{min}\cdot d_y,orgin_x+R_{max}\cdot d_y] \newline z:[O_z+R_{min}\cdot d_z,orgin_x+R_{max}\cdot d_z] \end{cases} $$
然后,基于上式计算结果和 AABB 包围盒在不同维度求交集即可,但是上述过程存在一个问题,计算机在计算过程中数据的范围存在一定限制,特别是当我们取光线传输范围 R 为 [0.001,INF] 的时候,存在浮点数溢出导致的错误结果,因而我们需要逆向计算,即通过 AABB 包围盒对应 XYZ 轴上的映射范围,求解此时 t 的约束范围 R’,然后利用 R’ 和原始的定义区间 R 求交集,判定是否在空间存在交集。这里以 X 轴计算为例,对应公式如下,其中 P 对应 x 轴上的一个临界区间边界
$$ t = \frac{P-O}{d_x} $$
3.1.4 更新
更新/删除 空间中物体可能存在位移或者形变,因而包围盒也需要动态维护,此时有两种策略更新或者重建,部分情况下重建是更好的选择,逐个更新可能导致 BVH 的平衡性受到破坏,退化成链式结构,导致低效的查询效率
插入 插入过程首先需要与当前的 BVH 进行求交判定当前插入的范围,若插入叶子结点则需要递归向上更新祖先的包围盒信息,部分情况下可能需要分裂叶子节点进行更新
3.1.5 其他内容
在计算部分,我们通过分解维度的方式规避了浮点数溢出带来的问题,但是另一方面也带来的新的问题临界问题(grazing condition)因而需要谨慎处理
在这里涉及 [[IEEE 浮点数运算]] 的部分规则,不过多展开,只讨论必要情况,右侧横排标题代表分子,左侧列排标题代表分母
| 0 | Num | |
|---|---|---|
| 0 | Nan | ♾ |
| Num | 0 | ✔ |
下面分别围绕这四种情况进行讨论
Num/Num 和 0/Num 情况很简单,麻烦在于分母为 0 时的情况。
此时分子不为 0 时,基于 IEEE 的浮点数运算规则,我们会根据正负号得到正无穷或者负无穷,这种情况出现在光线方向与某个坐标轴恰好垂直,导致其方向分量为 0。其可能对应情况如下,
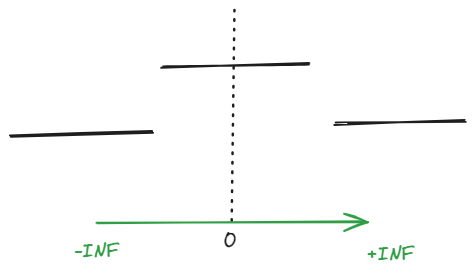
对于区间边界恰好跨过分界 0 的区间,我们可以计算得到正负无穷,可以用于和光线范围求交集,但是其他两种情况要么返回正无穷要么返回负无穷,无法进行区分,因而在这种情况下需要特判避免直接计算
而当分子分母均为 0 时,此时无法计算得到真正的值会返回结果 Nan。这种情况出现在光线方向与坐标轴垂直且出发点恰好位于临界区间边界。Nan 的存在非常特殊,Nan 与 任何数字比较均返回 false,因而也是需要进行特判单独计算。